Data-Flow-Analysis-Applications

Data Flow Analysis-Applications

这次笔记写的不是很细致，一些地方不清楚，等之后有时间了再修改，下周一开始笔记一周整理两次，并且转载一些高质量的帖子。

数据流分析概览

数据如何在CFG上流动？（How Data Flows on CFG）
这个问题可以理解为特定应用的数据如何在CFG的边（control flows）和结点(BBs/statements)上流动？特定应用相关的数据即对数据做抽象（Abstraction）,流动则是做Over-approxiamtion。绝大部分静态分析都是Over-approxiamtion（may analysis）。
may analysis 和 must analysis
may analysis: 输出的信息可能为真（over-approximation） must analysis: 输出的信息必须为真（under-approximation） Over-和under-approximation都是针对分析的安全性（正确性） Safe-approximation may analysis: safe=over must analysis：safe=under （没听懂）
结论
不同的数据流分析应用有不同的数据抽象和不同的flow safe-approximation策略，即不同的transfer functions和control-flow handlings。

数据流分析相关概念

输入输出状态（Input and Output States）
- 每次执行IR语句都会将输入状态转换成一个新的输出状态。（例如s1语句表示x=0,执行前x可能为其他值，执行后x=0）
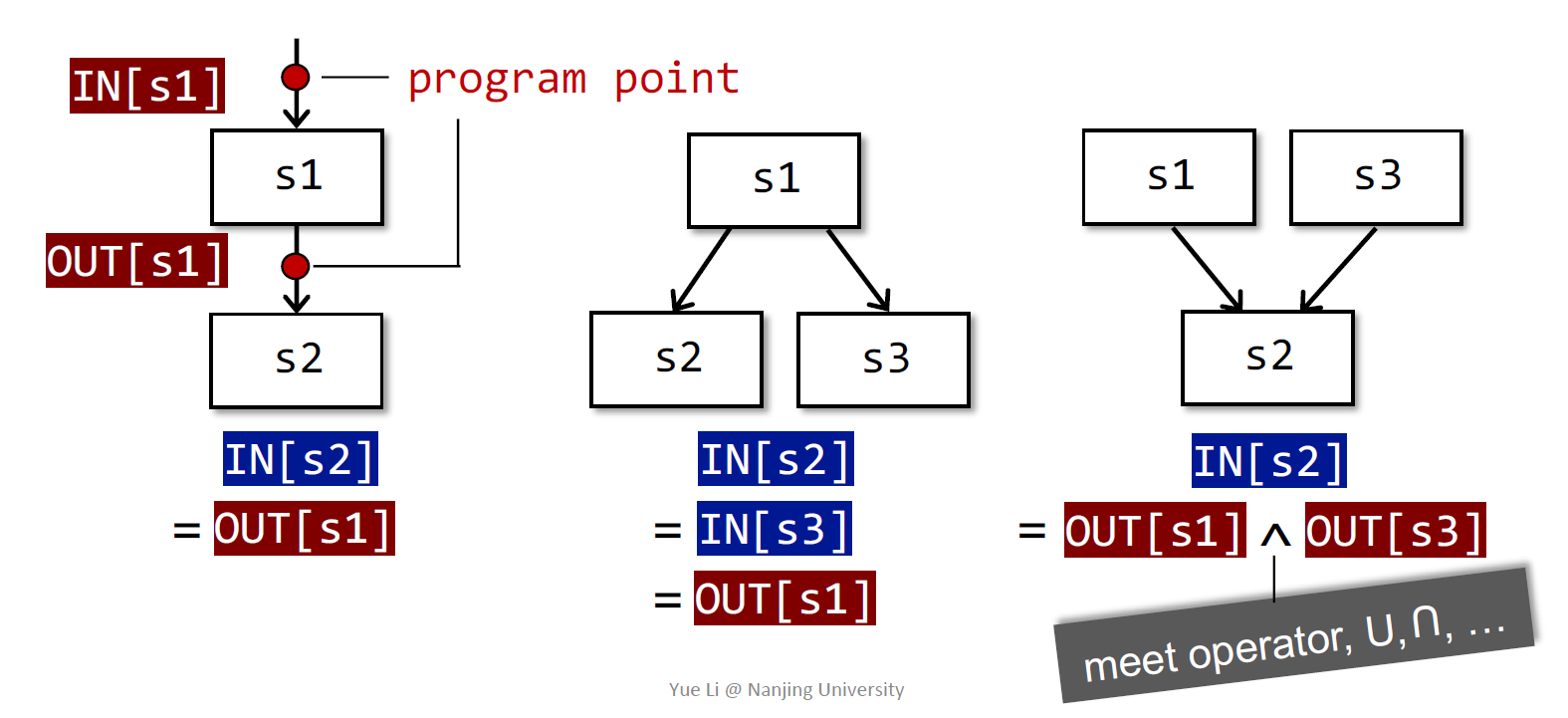
- 输入（输出）状态与语句之前（之后）的程序点相关联。(例如s1和s2是两个顺序执行的语句，IN[S2]=OUT[S1]，如果有分叉，IN[S2]=IN[S3]=OUT[S1]，如果汇聚，如下图示例，IN[S2]=OUT[S1]^OUT[S3])
如何从整体上把握静态分析
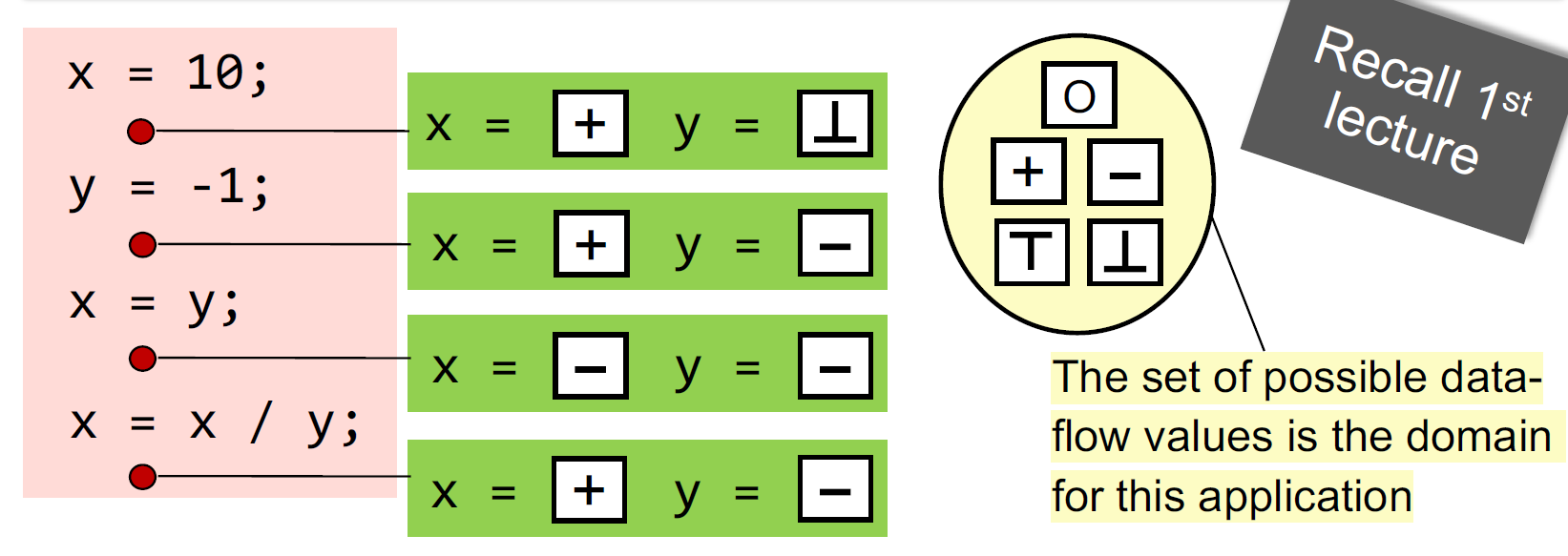
在每个数据流分析应用中，我们为每个程序点关联一个数据流值，该值代表对该点可以观察到的所有可能程序状态集的抽象。
如下图：
从宏观的角度重新审视下数据流分析，数据流分析旨在找到一个解决方案，通过解析一系列的Safe-approximation约束规则, 针对所有的语句得出IN和OUT。（个人理解，原句是Data-flow analysis is to find a solution to a set of safe-approximationdirected constraints on the IN[s]’s and OUT[s]’s, for all statements s.）约束规则主要是：
- 基于语句的语义（转换函数）的约束规则（constraints based on semantics of statements (transfer functions)）
- 基于控制流的约束规则（constraints based on the flows of control）
转换函数约束的表示
- Forward Analysis(前向分析)
  如下图：
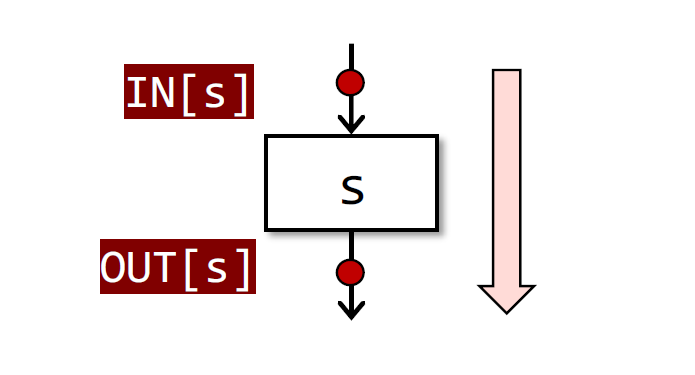
OUT[s] = f_s(IN[s])
- Backward Analysis(反向分析)
  如下图：
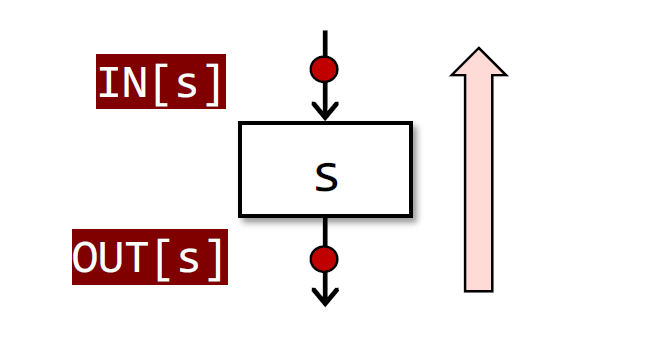
IN[s] = f_s(OUT[s])
控制流约束的表示
- BB内（Control flow within a BB）
  IN[s_i+1] = OUT[s_i]，for all i=1, 2, … , n-1
- BB之间(Control flow among BBs)
  IN[B] = IN[s₁]
  OUT[B] = OUT[s_n]
  针对汇聚的情况，如下图：
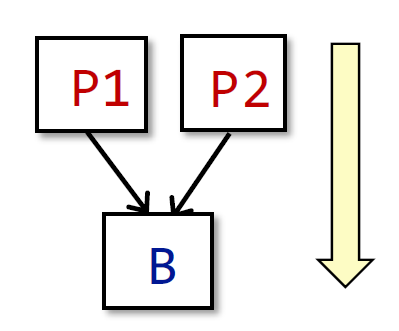
  其中， OUT[B] = f_B(IN[B])，f_B = f_{s_n} ° … ° f_s₂ ° f_s₁
  IN[B] = ^ P a predecessor of B OUT[P]
  Meet 运算符^用于总结不同的路径在路径汇合处的贡献。
  在反向分析的情况下，如下图：
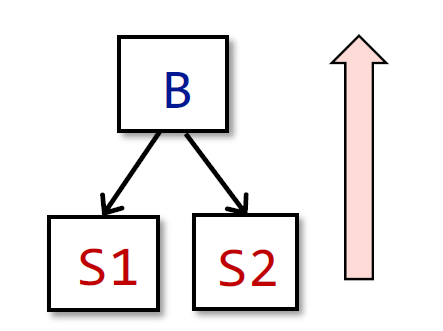
  IN[B] = f_B(OUT[B])，f_B = f_s₁ ° … ° f_{s_n-1} ° f_{s_n}
  OUT[B] = ^ S a successor of B IN[S]

可达定义分析（Reaching Definitions Analysis）

不会涉及的两方面的问题（包含下次笔记的两大分析，加上这些点会变复杂）
- 函数调用
  - 使用的CFG都是基于方法内的，不会涉及函数调用
  - 在涉及Inter-procedural Analysis的笔记时会介绍函数调用的内容
- 别名（Aliases）
  - 变量没有别名（别名：两个变量指向同一块内存会产生别名）
  - 将会在指针分析（指向分析，别名分析）中介绍
Reaching Definitions
定义: A definition d at program point p reaches a point q if there is a path from p to q such that d is not “killed” along that path.
解释：
1. A definition of a variable v is a statement that assigns a value to v （定义v的地方）
2. Translated as: definition of variable v at program point p reaches point q if there is a path from p to q such that no new definition of v appears on that path
示例：
在程序点p定义变量v的地方可以到达点q如果从p到q有一条路径，并且变量v在这条路径上没有被重新定义。
应用：
简单的错误检测（检测有可能未定义的变量）：
Reaching definitions can be used to detect possible undefined variables. e.g., introduce a dummy definition（label：undefine） for each variable v at the entry of CFG, and if the dummy definition of v reaches a point p where v is used, then v may be used before definition (as undefined reaches v)
简单来说就是未被定义的变量v可达程序点p，在p使用了变量v
Reaching Definitions是may analysis，不放过任何一条可能的路径。
Understanding Reaching Definitions
- 数据如何做Abstraction?
1. 一个程序中所有变量的定义需要做抽象
2. 可以使用位向量表示程序中变量的定义，如下图：
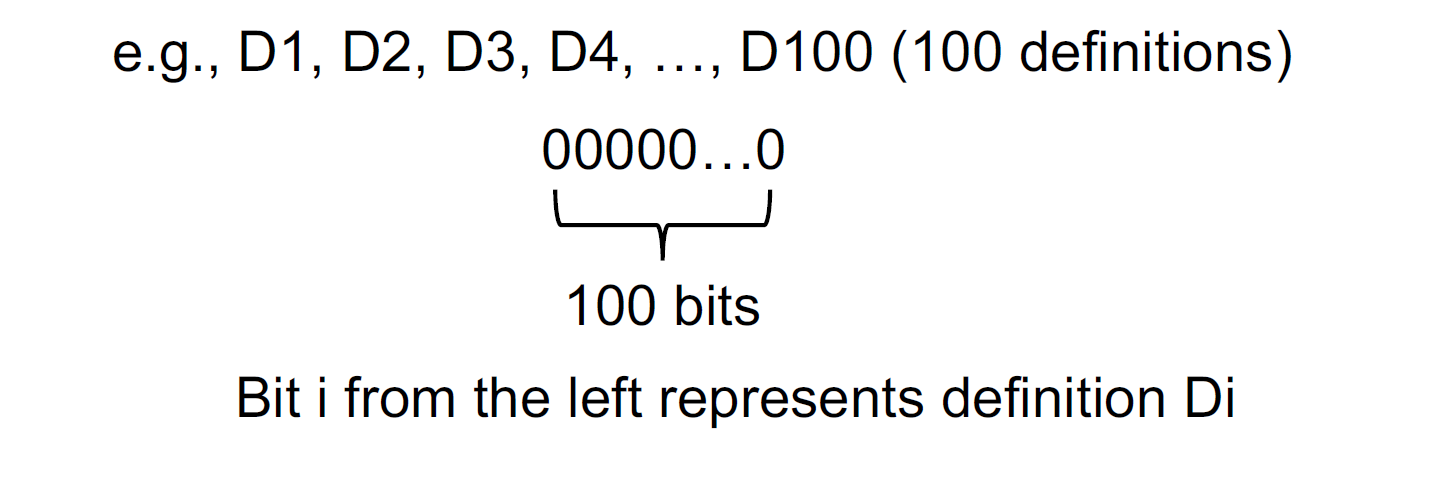
- 如何做Safe-approximation 例：
  从两个方面：
  - Transfer Function OUT[B]=gen_B U (IN[B]-kill_B) 图例：
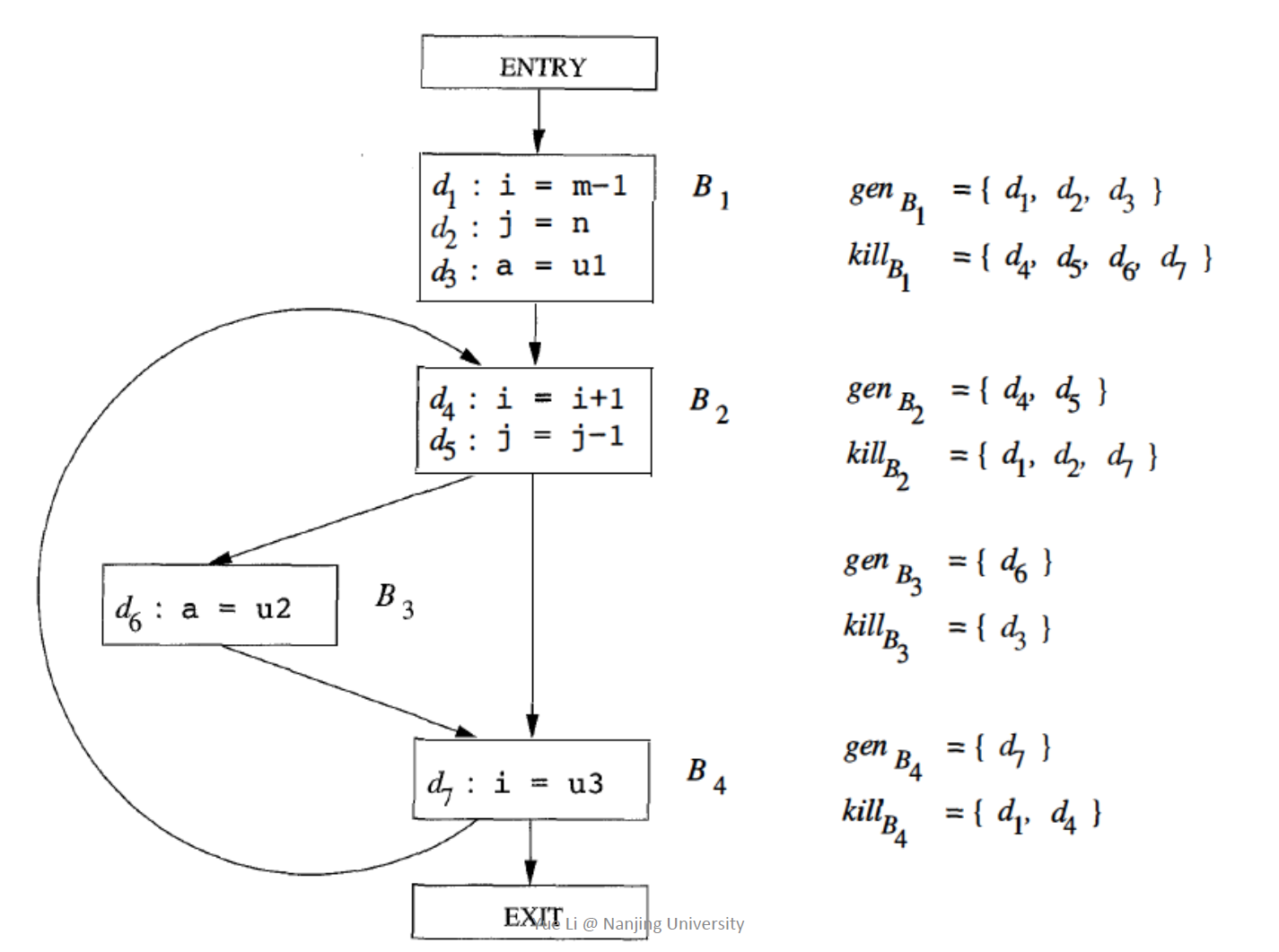
  - Control Flow IN[B]=UP a predecessor of B OUT[P]
可达定义分析算法